Baralho Alho

Pesquisadora Isadora adora jogar baralho com seus amigos. Mais especificamente, ela joga uma versão chamada Baralho Alho, em que há $N$ cartas (podendo haver cartas iguais). Inicialmente, as $N$ cartas estão em uma ordem especı́fica: a i-ésima carta tem valor $A_i$ . Duas cartas são consideradas iguais se possuem o mesmo valor.

Antes do jogo começar, Isadora declarou: “eu sempre embaralho Baralho Alho”. Ingenuamente, seus amigos toparam e deixaram que ela comandasse o embaralhamento. Mal sabem eles que Pesquisadora Isadora adora trapacear. Seu objetivo é embaralhar de tal forma que, ao final do processo, a i-ésima carta tenha valor $B_i$ .

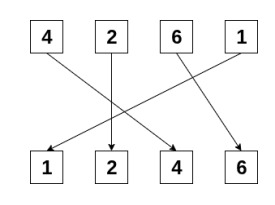
No entanto, ela conhece apenas um tipo de embaralhamento: aquele que faz a carta originalmente na posição $i$ ir para a posição $P_i$ . Por exemplo, se $P = [3, 2, 4, 1]$, então a primeira carta vai para a terceira posição, a segunda permanece na mesma, a terceira vai para a quarta e a quarta vai para a primeira. Assim, se o baralho inicial é $[4, 2, 6, 1]$, após aplicar o embaralhamento Isadora obtém $[1, 2, 4, 6]$.

Mesmo com essa limitação, Isadora é bastante inteligente e pensa em repetir o embaralhamento várias vezes para tentar alcançar novas configurações do baralho.

Escreva um programa que, dados $A_i$ , $B_i$ e $P_i$ , determine a menor quantidade de vezes que Isadora precisa aplicar o embaralhamento para que o baralho fique na ordem desejada. Caso isso seja impossível, imprima “IMPOSSIVEL” (sem aspas). Se o número mı́nimo de embaralhamentos for maior que 109 , imprima “DEMAIS” (sem aspas).

A primeira linha da entrada contém um inteiro$N (1 ≤ N ≤ 10^6 )$. A segunda linha contém $N$ inteiros $A_i$ $(1 ≤ A_i ≤ 10^9 )$, representando a configuração inicial do baralho. A terceira linha contém $N$ inteiros $B_i (1 ≤ B_i ≤ 10^9 )$, representando a configuração final desejada do baralho. A quarta linha contém $N$ inteiros distintos $P_i (1 ≤ P_i ≤ N )$, indicando que a carta na posição $i$ vai para a posição $P_i$ após uma aplicação do embaralhamento.

Imprima um único inteiro $k$: o menor número de vezes que o embaralhamento deve ser aplicado, a partir de $A_i$ , até que a configuração obtida seja $B_i$ . Se isso for impossível, imprima “IMPOSSIVEL” (sem aspas). Se o menor $k$ for maior que 10^9 , imprima “DEMAIS” (sem aspas).