Dominós
Alice, cansada de sair com seus amigos, inventou sua própria variação do famoso jogo de dominó. Sua versão usa o mesmo conjunto de peças de dominó que o jogo tradicional, em que cada peça é uma ficha que mostra dois números entre um e seis, com um número em cada extremidade.
Para começar o jogo, Alice embaralha as peças de dominó em uma pilha e então pega uma peça de cada vez do topo. Quando Alice pega a primeira peça da pilha, ela simplesmente a coloca na mesa. Da segunda peça em diante, ela precisa colocá-la no lado esquerdo ou no direito da corrente formada pelas peças já na mesa.
Para colocar uma peça em uma extremidade da corrente, um de seus números deve corresponder ao número naquela extremidade. O outro número da peça recém-jogada se torna a nova extremidade livre da corrente. Se Alice não conseguir colocar uma peça, ela perde o jogo; caso contrário, se conseguir colocar todas as peças com sucesso, ela vence.
Alice não está interessada em jogos que não pode vencer, então ela gostaria de saber se é possível vencer com um determinado conjunto de dominós. Além disso, ela pode não ter um conjunto completo, pois pode ter perdido algumas peças.
Como Alice pode escolher jogar com um subconjunto de suas peças (efetivamente descartando o restante para tornar o jogo vencível), você deve calcular o número total de subconjuntos de seus dominós para os quais existe uma chance não nula de vitória.
Input
A entrada contém múltiplos casos de teste. A primeira linha contém um inteiro $T (1 ≤ T ≤ 10^4 )$, o número de casos de teste. Cada caso de teste é descrito da seguinte forma:
A primeira linha do caso contém um inteiro $N (1 ≤ N ≤ 21)$, o número de peças que Alice possui.
As N linhas seguintes contêm dois inteiros $a_i$ e $b_i$ $(1 ≤ a_i ≤ b_i ≤ 6)$, indicando que a i-ésima peça de dominó que Alice possui contém os números $a_i$ e $b_i$ .
É garantido que Alice não possui peças duplicadas; em outras palavras, $(a_i , b_i ) \ne (a_j , b_j )$ se $i \ne j$.
Output
Para cada caso de teste, imprima uma única linha contendo um inteiro: o número de subconjuntos de peças com os quais Alice tem uma chance não nula de vencer.
3 3 1 2 2 3 3 4 4 1 1 1 2 2 3 3 4 3 1 2 2 2 2 3
6 10 7
Explanation 1:
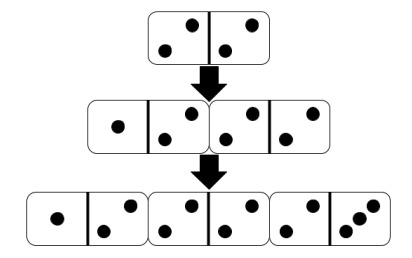
Para o terceiro caso de entrada, temos as peças 1-2, 2-2 e 2-3. Considerando o subconjunto em que todas as peças estão presentes, uma ordem possível para as peças retiradas da pilha após o embaralhamento é a mostrada na imagem: 2-2, seguida de 1-2 e, por fim, 2-3.
Nessa ordem, Alice pode colocar a peça 1-2 à esquerda da 2-2 e, em seguida, a 2-3 à direita, como ilustrado na imagem. Portanto, para este subconjunto, a chance de Alice vencer não é nula.
2 1 2 6 3 5 5 2 2 2 3
1 4