Gerador universal

Sandy está desenvolvendo um novo computador como parte do ambicioso projeto Sistema Binário Compactador (SBC). Esse projeto faz parte de um grande desafio tecnológico conhecido como Interface de Codificação por Padrões Compactos (ICPC), cuja meta é atingir a máxima eficiência na escrita de grandes volumes de dados.

A proposta do SBC é ousada: escolher um padrão-base $B$, formado por 8 bits $b_0, \dots, b_7$ e, a partir dele, gerar qualquer outro padrão aplicando apenas algumas operações simples e rápidas.

Sandy deseja escrever na memória uma sequência de $N$ bits, com $N \geq 8$, denotada por $C = c_0, \dots, c_{N-1}$. Inicialmente, a memória está preenchida apenas com zeros. Em seguida, ela pode repetir a seguinte operação quantas vezes quiser:

• Escolha um número inteiro $i$ entre $-7$ e $N-1$, a posição onde $B$ será aplicado;
• Para cada posição de $B$ alinhada com a mensagem, isto é, para todo $j$ de $0$ a $7$ tal que $0 \leq i + j \leq N - 1$, substitua o conteúdo de $c_{i+j}$ pelo resultado de $b_j \oplus c_{i+j}$, onde $\oplus$ representa a operação XOR (ou “ou-exclusivo”).

O exemplo a seguir ilustra duas aplicações do procedimento acima. Aplicando o padrão $B$ a um conteúdo $C$, obtém-se o resultado final $C'$.

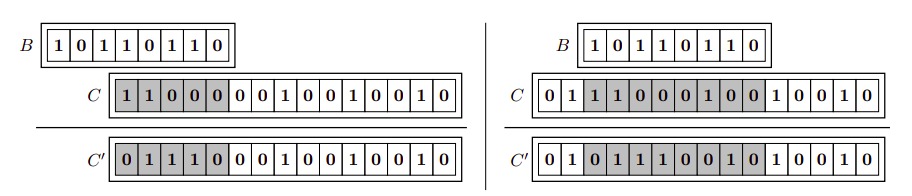
Como os dados que desejamos escrever na memória geralmente não são aleatórios, Sandy acredita que, com uma boa escolha do padrão-base $B$, será possível produzir o conteúdo desejado com poucas operações.

Para testar essa hipótese, ela precisa da sua ajuda: dado o conteúdo $C$ que deve ser escrito na memória, determine o padrão-base $B$ que minimiza o número de operações necessárias para gerar $C$ conforme descrito, e também a quantidade $Q$ de operações necessárias.

Pode-se provar que é sempre possível escrever qualquer conteúdo usando esse procedimento. Porém, para que o projeto SBC seja bem-sucedido e conquiste o selo de excelência do ICPC, a sua solução precisa ser rápida e eficiente!

A primeira linha contém um inteiro $N$ ($8 \leq N \leq 4096$), o comprimento de $C$. A segunda linha contém uma sequência de $N$ bits $C$, representando o conteúdo que deve ser escrito na memória.

Seu programa deve produzir uma única linha contendo:

• uma sequência de 8 bits $B$, representando o padrão-base que minimiza o número de operações necessárias, e
• um inteiro $Q$, representando o número mínimo de operações.

Se houver mais de um padrão $B$ que minimize o número de operações, imprima aquele que corresponder ao menor valor inteiro em base 2, considerando $b_0$ como o bit mais significativo e $b_7$ como o menos significativo.