Investigação Cósmica

A Sociedade Brasileira de Cosmonáutica (SBC) está treinando suas equipes para a próxima edição da Investigação Cósmica de Planetas Celestes (ICPC).

A SBC fará uma exploração simulada de uma galáxia distante chamada Quadradômeda. Para esta missão, foram selecionadas $N$ estrelas, por sua localização geometricamente estratégica, e foi determinada a ordem de visitação, identificada pela numeração de $1$ a $N$. Para preparar as equipes, modelos simplificados são utilizados, nos quais cada estrela é representada por um ponto no plano com coordenadas inteiras $(x_i, y_i)$.

As estrelas estão dispostas de forma que, para cada $1 \leq i < N$, a estrela $i$ está alinhada com a estrela $i+1$, ou seja, compartilham a mesma coordenada $x$ ou a mesma coordenada $y$.

O objetivo da missão é orbitar cada estrela $i$ em uma circunferência de raio inteiro constante $R_i \geq 1$. Durante a simulação, a nave orbita a estrela atual e, ao atingir o ponto da órbita mais próximo da próxima estrela, abandona essa órbita e passa a orbitar a estrela seguinte imediatamente.

Para que essa manobra seja possível, para cada $1 \leq i < N$, o raio $R_i$ deve ser estritamente menor que a distância euclidiana entre as estrelas $i$ e $i+1$.

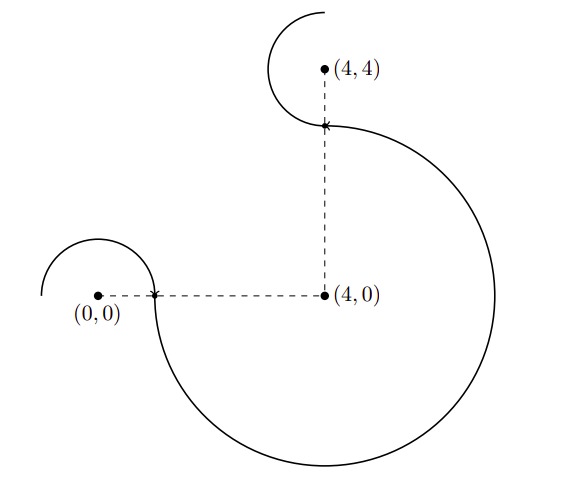
No exemplo abaixo, é ilustrada uma configuração válida de órbitas, em que $N = 3$ e as estrelas estão nos pontos $(0,0)$, $(4,0)$ e $(4,4)$. Na configuração exibida, temos $R_1 = 1$, $R_2 = 3$ e $R_3 = 1$.

(0,0)
(4,0)
(4,4)

Sua tarefa é determinar o maior valor inteiro possível de $R_1$ tal que seja possível escolher valores $R_1, R_2, \dots, R_N$ que satisfaçam todas as condições descritas. Caso não exista nenhuma configuração válida de órbitas, informe que a missão é impossível.

A primeira linha contém um inteiro $N$ ($2 \leq N \leq 10^5$), o número de estrelas.

Cada uma das próximas $N$ linhas contém dois inteiros $x_i$ e $y_i$ ($|x_i|, |y_i| \leq 10^9$), representando as coordenadas da estrela $i$. Para cada $1 \leq i < N$, as estrelas $i$ e $i+1$ estão alinhadas horizontal ou verticalmente.

Seu programa deve produzir uma única linha contendo o maior valor inteiro possível para $R_1$ tal que exista uma configuração válida de órbitas, ou -1 caso a missão seja impossível.