Lonely Creatures
There are $N$ creatures, numbered from 1 to $N$, that live in an infinite city represented by the 2D plane. Creature $i$ lives on the straight line $y=M_{i}\cdot x+C_{i}$; it may move anywhere along that line. No two creatures share the same line, but a meeting occurs if their lines intersect. In that case, the intersection point is called a meeting point of the two creatures.
The city has just built a new playground. The playground's boundary is the (axis-aligned) parabola $y=A\cdot x^{2}+B$ where $A>0$. The playground is the open region $y>A\cdot x^{2}+B$, so points exactly on the boundary are not inside the playground.
Now the city officials want to know whether the new playground is reducing loneliness, and that's where your help is needed. Your task is to count how many distinct pairs of creatures have a meeting point that lies strictly inside the playground. Each pair is counted once; the order of the creatures in a pair does not matter.
Explanation of sample 1 :
Creature 1 meets creatures 2 and 3, but in both cases the meeting point lies outside the playground. There are no other meeting points, so the answer is 0.
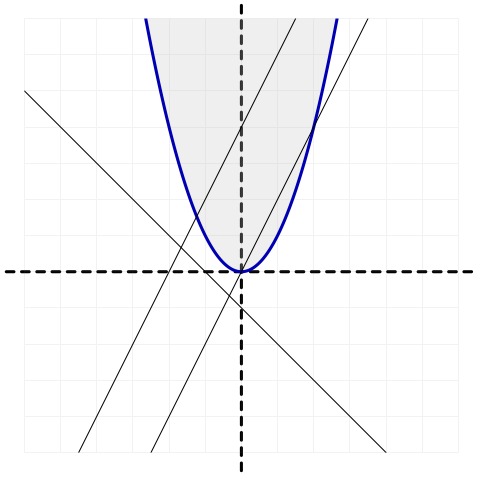
Input
The first line contains three integers $N$ $(2\le N\le10^{5})$, $A$ $(1\le A\le10^{4})$ and $B(-10^{4}\le B\le 10^{4})$, indicating that there are $N$ creatures and that the playground is the open region of the 2D plane $y>A\cdot x^{2}+B$. Each creature is identified by a distinct integer from 1 to $N$.
The $i$-th of the next $N$ lines contains two integers $M_{i}$ and $C_{i}(-10^{4}\le M_{i},C_{i}\le10^{4})$, representing that creature $i$ lives on the straight line $y=M_{i}\cdot x+C_{i}$. It is guaranteed that no two lines are identical.
Output
Output a single line with an integer indicating the number of distinct pairs of creatures whose meeting point lies strictly inside the playground.
3 1 0 -1 -1 2 4 2 0
0
4 1 -2 -1 0 0 1 1 0 2 1
5
Explanation 2:
Each pair of creatures have a meeting point.
However, the meeting point of creatures 3 and 4 lies on the playground boundary $(y = A * x^2 + B)$, so that pair is excluded from the count.
4 1 0 7 -3 5 -2 3 -1 1 0
6