Jornada Colorida

No paı́s de Oz as estradas são pavimentadas com pedras coloridas. Cada estrada conecta exatamente duas cidades, pode ser percorrida nos dois sentidos e é colorida com pedras de uma única cor. Dorotéia está visitando Oz pela primeira vez e deseja realizar um passeio pelo paı́s, atendendo às seguintes condições:

• O passeio deve iniciar e terminar numa mesma cidade.

• O passeio deve passar por cada estrada do paı́s exatamente uma vez e não pode usar duas estradas consecutivas (ou seja, uma imediatamente após a outra) que tenham a mesma cor.

• A primeira e última estrada do passeio devem ter cores diferentes.

A figura (a) abaixo ilustra um exemplo com cinco cidades e seis estradas. A figura (b) mostra um possı́vel passeio que inicia e termina na cidade 2 e satisfaz as restrições de cores das estradas. Na figura (b), o passeio inicia da cidade 2 e percorre, em sequência, as estradas 1 (vermelha), 3 (verde), 4 (azul), 2 (vermelha), 6 (azul) e, finalmente, 5 (verde).

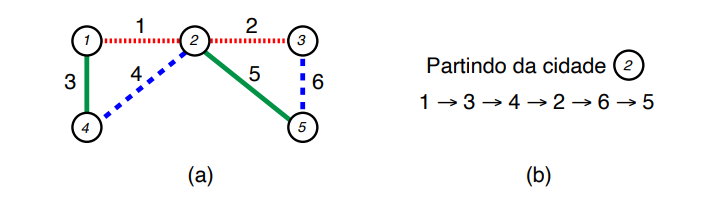
Ajude Dorotéia a encontrar tal passeio ou, se não for possı́vel, indique que não existe.

A primeira linha da entrada contém três inteiros, $N$ , $M$ e $K$, representando respectivamente o número de cidades $(2 ≤ N ≤ 1000)$, o número de estradas $(1 ≤ M ≤ 1000)$ e o número de cores $(1 ≤ K ≤ 1000)$. As cidades são identificadas por inteiros de $1$ a $N$ , as estradas são identificadas por inteiros de $1$ a $M$ e as cores são identificadas por inteiros de $1$ a $K$.

Cada uma das $M$ linhas seguintes descreve uma estrada e contém três inteiros $I$, $J$ e $C$, onde $I$ e $J$ representam cidades $(1 ≤ I, J ≤ N$ e $I \neq J)$, e $C$ indica a cor da estrada $1 ≤ C ≤ K$. As estradas são dadas na ordem de sua identificação, ou seja, a primeira estrada da entrada é a de número 1, a segunda estrada é a de número 2, e assim por diante.

Caso não exista passeio que satisfaça as restrições, imprima um único inteiro −1. Caso contrário, seu programa deve produzir duas linhas descrevendo um passeio válido. A primeira linha deve conter o identificador da cidade inicial do passeio. A segunda linha deve conter $M$ inteiros distintos, cada um identificando uma estrada, na ordem do passeio. Se houver mais de um passeio possı́vel, imprima qualquer um deles.