Esculpindo triangulos

Seu amigo é um escultor renomado em todo o país, conhecido por criar algumas das melhores obras de arte que o mundo moderno já viu. No entanto, ele agora enfrenta um grande desafio: esculpir o maior triângulo possível em um bloco de mármore, para ser exibido no museu de obras abstratas.

A tarefa seria simples se ele pudesse adquirir um bloco de mármore retangular para iniciar o trabalho. Contudo, a marmoaria de onde os blocos são adquiridos vende apenas peças irregulares, que não correspondem exatamente às dimensões planejadas. Esses blocos são extraídos de pedreiras e apresentam um lado plano e bem polido, enquanto o outro pode sofrer danos durante o processo de extração, resultando em formas irregulares.

Uma peça de mármore pode ser representada como uma série de colunas com alturas variadas. Observando essas peças, você percebeu que ainda é possível esculpir um triângulo, aproveitando ao máximo o material disponível. Abaixo está um exemplo de uma peça de mármore e do maior triângulo que pode ser extraído dela:

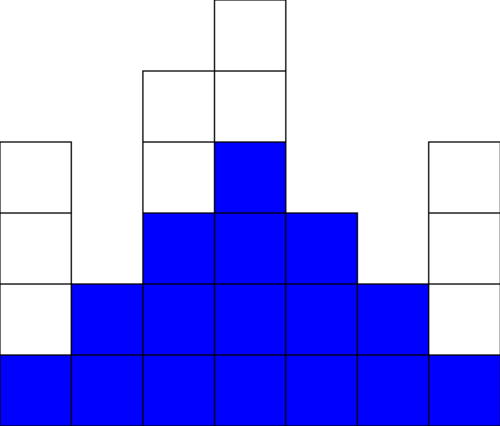
Regras para esculpir o triângulo:

• A altura do triângulo será definida pela altura do seu ponto central.
• Para formar o triângulo desejado, a diferença de altura entre colunas adjacentes não pode ser maior que um bloco.
• Para qualquer coluna do triângulo, as colunas adjacentes devem ter altura maior ou igual à altura da coluna atual menos 1.

Problema:

Desenvolva um programa que, dada uma peça de mármore representada como uma sequência de alturas, determine a altura do maior triângulo que pode ser esculpido a partir dela.

Será dadao um $N$, representando a quantidade de colunas, seguido por $N$ valores $a_i$ representando a altura de cada coluna da peça de marmore. $(1 \le N \le 10^6) (0 \le a_i \le 10^9)$

A saida deve ser a altura do maior triangulo que é possivel extrair da peça de marmore.