Fundindo árvores

Em Computação árvores são objetos estranhos: a raiz está no topo e as folhas estão embaixo! Uma árvore é uma estrutura de dados composta de $N$ vértices conectados por $N − 1$ arestas de forma que é possı́vel chegar de um vértice a qualquer outro vértice seguindo as arestas. Em uma árvore enraizada, cada aresta conecta um vértice pai a um vértice filho. Um único vértice não tem pai, e é chamado de raiz. Assim, partir da raiz é possivel chegar a qualquer outro vértice da árvore seguindo as arestas na direção de pai para filho.

Em uma árvore ternária cada vértice pode ter até três vértices filhos, chamados esquerdo, central e direito. Uma árvore ternária canhota é uma árvore ternária enraizada em que nenhum vértice tem filho direito. Uma árvore ternária destra é uma árvore ternária enraizada em que nenhum vértice tem filho esquerdo. A raiz de uma árvore ternária é sempre um vértice central. A figura abaixo mostra exemplos de uma árvore canhota e de uma árvore destra.

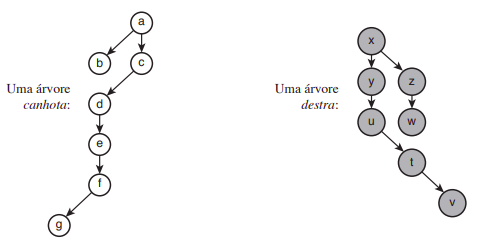
A superposição $S$ de uma árvore canhota $C$ com uma árvore destra $D$ é uma árvore ternária enraizada em que a raiz é ou a raiz de $C$ ou a raiz de $D$ ou ambas as raı́zes, de $C$ e de $D$, superpostas, e que contém a estrutura de ambas as árvores superpostas. A figura abaixo mostra algumas árvores formadas pela superposição da árvore canhota e da árvore destra da figura acima.

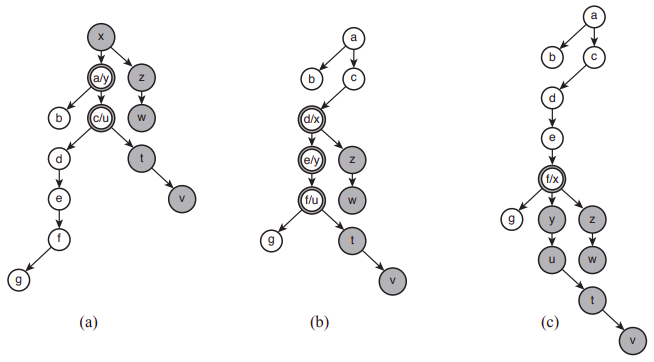
Note que na Figura (a) a raiz é o vértice $x$ (da árvore destra) e os pares de vértices ($a, y$) e ($c, u$) são superpostos. Na Figura (b) a raiz é o vértice $a$ (da árvore canhota) e os pares de vértices ($d, x$), ($e, y$) e ($f, u$) são superpostos. Na Figura (c) a raiz também é o vértice a (da árvore canhota) e o par de vértices ($f, x$) é superposto.

Dadas uma árvore canhota e uma árvore destra, sua tarefa é determinar o número mı́nimo de vértices necessários para construir uma árvore ternária que é uma superposição das árvores dadas.

A primeira linha de um caso de teste contém um inteiro $N$ indicando o número de vértices da árvore canhota $(1 ≤ N ≤ 10^4 )$. Vértices nesta árvore são identificados por números de $1$ a $N$, e a raiz é o vértice de número $1$. Cada uma das $N$ linhas seguintes contém três inteiros $I$, $L$ e $K$, indicando respectivamente o identificador de um vértice $I$, o identificador do filho esquerdo $L$ de $I$ e o identificador do filho central $K$ de $I$ $(0 ≤ I, L, K ≤ N )$.

A linha seguinte contém um inteiro $M$ indicando o número de vértices da árvore destra $(1 ≤ M ≤ 10^4 )$. Vértices nesta árvore são identificados por números de $1$ a $M$ , e a raiz é o vértice de número 1. Cada uma das $M$ linhas seguintes contém três inteiros $P$ , $Q$ e $R$, indicando respectivamente o identificador de um vértice $P$, o identificador do filho central $Q$ de $P$ e o identificador do filho direito $R$ de $P$ $(0 ≤ P, Q, R ≤ N )$.

Obs: O valor zero indica um vértice não existente (usado quando um vértice não tem um ou ambos os seus filhos).

Imprima o número mı́nimo de vértices de uma árvore que é a superposição das duas árvores dadas na entrada.