Go--

Go−− é até parecido com o tradicional jogo de Go, mas é bem mais fácil! Ele é jogado em um tabuleiro quadrado de dimensão $N$, inicialmente vazio, no qual dois jogadores, um jogando com as pedras pretas e o outro com as brancas, se alternam colocando uma pedra por vez dentro de qualquer célula que ainda não esteja ocupada. A partida termina depois que cada jogador colocou $P$ pedras no tabuleiro. Considere todas as possı́veis sub-áreas quadradas de dimensão de $1$ a $N$. Uma sub-área pertence ao jogador que joga com as pedras pretas se ela contém pelo menos uma pedra preta e nenhuma pedra branca. Da mesma forma, uma sub-área quadrada pertence ao jogador que joga com as pedras brancas se contém ao menos uma pedra branca e nenhuma pedra preta. Note que as áreas que não contenham nenhuma pedra, ou que contenham tanto pedras pretas quanto brancas, não pertencem a nenhum jogador.

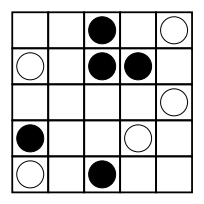
Neste problema, dada a posição final do tabuleiro, seu programa deve computar quantas sub-áreas quadradas pertencem a cada jogador, para descobrir quem ganhou a partida. Na figura, as pretas possuem 12 sub-áreas (cinco de dimensão 1, seis de dimensão 2 e uma de dimensão 3). As brancas, que perderam a partida, possuem apenas 10.

A primeira linha da entrada contém dois inteiros $N$ e $P$ , $2 ≤ N ≤ 500$, $1 ≤ P ≤ 500$ e $P ≤ N^2 /2$, representando, respectivamente, a dimensão do tabuleiro e o número de pedras que cada jogador coloca. Cada uma das P linhas seguintes contém dois inteiros $L$ e $C$ $(1 ≤ L, C ≤ N)$ definindo as coordenadas (linha, coluna) das pedras pretas. Depois, cada uma das próximas $P$ linhas contém dois inteiros $L$ e $C$ $(1 ≤ L, C ≤ N )$ definindo as coordenadas (linha, coluna) das pedras brancas. Todas as pedras são colocadas em células distintas.

Imprima uma linha contendo dois inteiros separados por um espaço: quantas áreas distintas pertencentes às pretas e às brancas.