Kit de encolhimento de polígonos

Um Kit de Encolhimento de Polı́gonos é um material muito utilizado nas aulas de magia geométrica na Nlogônia. O kit consiste de dois pontos, $A$ e $B$ no plano cartesiano. Considere um polı́gono convexo dado pelos vértices $1, 2...N$ , nessa ordem. Para encolher esse polı́gono usando o kit, algumas regras devem ser respeitadas. Cada vértice $x$ do polı́gono deve ser movido uma vez só: para o ponto médio do segmento $A_x$ ou para o ponto médio do segmento $B_x$. A operação de encolhimento deve produzir um novo polı́gono convexo que preserve a ordem relativa dos vértices do polı́gono original. Em outras palavras, considerando todas as possı́veis maneiras de aplicar o kit, apenas aquelas cuja sequência final dos vértices $1, 2...N$ representa um polı́gono convexo são válidas. Veja que o polı́gono convexo original pode estar em sentido horário e uma operação de encolhimento válida produzir um polı́gono convexo em sentido anti-horário, na mesma ordem dos vértices. Apenas a ordem relativa dos pontos é importante, não o sentido.

É sabido que magia geométrica não é o forte da maioria dos alunos. A professora pediu que eles usassem o kit de encolhimento para encolher um polı́gono convexo fornecido por ela de forma a obter a menor área possı́vel e um amigo seu implorou para que você resolva a questão por ele. Responda a menor área possı́vel do polı́gono para ele.

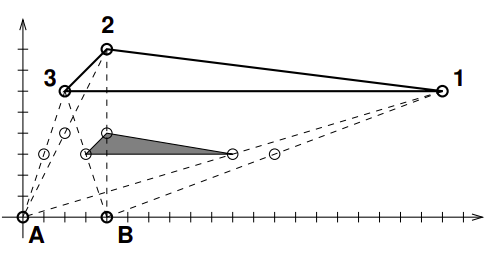
A Figura acima ilustra um uso válido do kit, onde o polı́gono sombreado é o de menor área possı́vel que preserva a sequência dos vértices. Os pontos A e B correspondem aos pontos do kit. Note que, apesar do nome encolhimento, às vezes é possı́vel utilizar o kit para aumentar a área dos polı́gonos! Como geometria é difı́cil!

Observe que um único ponto ou uma reta não são considerados polı́gonos. Sendo assim, se um uso do kit produzir como resultado algo diferente de um polı́gono convexo, esse não é um uso válido.

A primeira linha da entrada contém um inteiro $N$ $(3 ≤ N ≤ 10^5 )$, o número de vértices do polı́gono. Seguem $N$ linhas, cada uma com dois inteiros $x, y$ $(−10^6 ≤ x, y ≤ 10^6 )$, os vértices do poligono.

A última linha da entrada contém quatro inteiros, $A_x$ , $A_y$ , $B_x$ e $B_y$ $(−10^6 ≤ A_x , A_y , B_x , B_y ≤ 10^6 )$, as coordenadas $x$ e $y$ de $A$ e as coordenadas $x$ e $y$ de $B$, respectivamente.

Os pontos da entrada serão dados na ordem correta em que aparecem no polı́gono, no sentido horário ou anti-horário. Não haverão pontos repetidos e o polı́gono será convexo.

Seu programa deve produzir uma linha, contendo um número real, com 3 casas decimais de precisão, representando a menor área possı́vel para um polı́gono obtido com o uso do kit.