Circuitos Lógicos Matriciais
Na computação quântica, as portas lógicas funcionam de um jeito um pouco diferente. Portas lógicas quânticas são reversíveis e o número de qubits de entrada é igual ao número de qubits de saída. Além disso, elas podem ser representadas por matrizes $2^N$ por $2^N$ , onde $N$ é o número de qubits.
Um circuito quântico é um modelo para computação quântica onde a computação é realizada através de uma sequência de portas lógicas quânticas e dispositivos de medição. Uma sequência de portas lógicas pode ser representada por uma matriz resultante da multiplicação das matrizes das portas lógicas em ordem de aplicação, que é a ordem inversa de como elas são representadas gramácamente. Por exemplo, o circuito de adição de dois bits em seu forma quântica é:
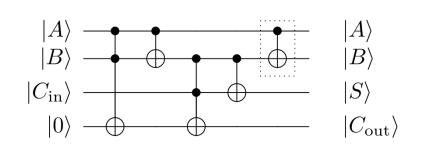
Temos nesse circuito duas variações de uma porta lógica que chamaremos de $CNOT(q_c, q_t )$ e $CCNOT(q_{c1} , q_{c2} , q_t )$. No desenho, o qubit $q_t$ aparece marcado com um ⊕. A porta lógica $CNOT(q_c , q_t )$ pode ser vista como sendo igual a $CCNOT(q_c , q_c , q_t )$, ou seja, a aplicação da porta lógica $CCNOT$ com $q_c = q_{c1} = q_{c2}$ . A porta lógica $CCNOT(q_{c1} , q_{c2} , q_t )$ tem o comportamento de inverter o qubit $q_t$ da saída se os qubits de controle $q_{c1}$ e $q_{c2}$ ambos estiverem ligados. Matematicamente, $q_t′ = q_t ⊕ (q_{c1} ∧ q_{c2} )$. Na sua forma de matriz,

onde $i$ é a linha e $j$ a coluna com $0 ≤ i, j < 2^N$ , e $i$ contém o bit $k$ $(0 ≤ k)$ se $\frac{x}{2^k} \mod 2 = 1$. A
operação ⊕ é a operação bit a bit de ou exclusivo, comumente o ∧ em linguagens de programação.
Desta forma, a matriz do circuito quântico de adição de dois bits é dada por $CNOT(q_0 , q_1 )$ $CNOT(q_1 , q_2 )$ $CCNOT(q_1 , q_2 , q_3 )$ $CNOT(q_0 , q_1 )$ $CCNOT(q_0 , q_1 , q_3 )$,
onde os qubits $q_0 , q_1 , q_2 , q_3$ são utilizados com entrada $|A⟩ , |B⟩ , |C_{in}⟩ , |0⟩$ respectivamente e resultam em $|A⟩ , |B⟩ , |S⟩ , |C_{out}⟩$ respectivamente.
Sua missão é dada a descrição de um circuito com portas lógicas $CNOT$ e $CCNOT$ na ordem de aplicação, imprimir a matriz resultante.
Input
A primeira linha da entrada contém os inteiros $N$ $(2 ≤ N ≤ 8)$, o número de qubits do circuito e $M$ $(1 ≤ M ≤ 10^5 )$, a quantidade de portas lógicas do circuito.
Seguem $M$ linhas, cada uma com a descrição de uma porta lógica. O primeiro inteiro $T$ $(1 ≤ T ≤ 2)$ define o tipo da porta lógica. Se $T = 1$, a descrição é da porta lógica $CNOT(q_C , q_T )$ e seguem os inteiros distintos $C$ e $T$ $(0 ≤ C, T < N )$. Se $T = 2$, a descrição é da porta lógica $CCNOT(q_{C_1} , q_{C_2} , q_T )$ e seguem os inteiros distintos $C_1$ , $C_2$ e $T$ $(0 ≤ C_1 , C_2 , T < N )$. Note que as portas lógicas são dadas na ordem de aplicação.
Output
Imprima $2^N$ linhas, cada uma com exatamente $2^N$ caracteres 0 ou 1, correspondendo a matriz do circuito quântico completo.
2 1 1 0 1
1000 0001 0010 0100
Explanation 1:
Este circuito representa apenas a porta lógica $CNOT(c,t)$. Se você já leu sobre essa porta lógica,
a matriz parece estar errada pois é diferente da que está na literatura. Porém, é uma questão de
convenção. Ao compormos o qubit $c$ com o qubit $t$, aqui estamos usando a convenção de que o
primeiro bit é menos significante que o segundo.
Então se entrada for $|00⟩$ ou $|10⟩$, ambos onde $c = 0$ e $t$ varia, a porta lógica não atua. Quando a entrada é $|01⟩$ ou $|11⟩$, então a porta lógica atua e inverte o valor de $t$. Essa convenção é utilizada por exemplo pela biblioteca Qiskit.
4 5 1 0 1 1 1 2 2 1 2 3 1 0 1 2 0 1 3
1000000000000000 0000000000000100 0000000000000010 0000000000010000 0000100000000000 0100000000000000 0010000000000000 0000000000000001 0000000010000000 0000010000000000 0000001000000000 0001000000000000 0000000000001000 0000000001000000 0000000000100000 0000000100000000
3 1 2 0 1 2
10000000 01000000 00100000 00000001 00001000 00000100 00000010 00010000
3 1 1 0 1
10000000 00010000 00100000 01000000 00001000 00000001 00000010 00000100